Глава 5.
АНАЛИЗ СИСТЕМАТИЧЕСКИХ ОШИБОК ЗВЕЗДНОГО КАТАЛОГА.
§3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ γ(t) И φ(t) МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ.
Найдем решение γ(t) и φ(t) задачи минимизации (5.2.4), (5.2.5). Ниже, в конкретных примерах, эта задача рассматривается для совокупностей, состоящих из различного количества звезд. Поэтому в расчетах мы будем использовать следующие нормированные величины, в которых N означает число звезд в изучаемой совокупности:
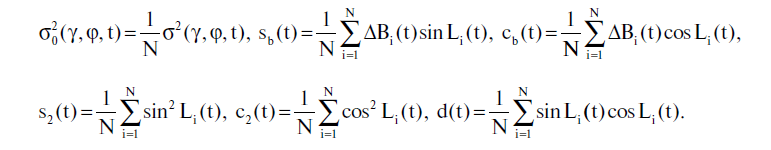
Отметим, что все эти величины могут быть вычислены для любого момента времени t, исходя из значения современных координат звезд и координат звезд в каталоге Альмагеста.
Очевидно, что задача минимизации (5.2.4) эквивалентна задаче минимизации
| σ02(γ, φ, t) → min | (5.3.1) |
в том смысле, что параметры γ(t) и φ(t), определяемые соотношением (5.3.1), совпадают с параметрами, определяемыми решением задачи (5.2.4).
Как отмечалось, решение задачи (5.3.1) имеет смысл лишь для больших совокупностей звезд, и поскольку ниже мы будем изучать статистические свойства этого решения, то здесь и далее через γstat(t) и φstat(t) обозначаются величины, удовлетворяющие соотношению (5.3.1).
Значение
| σmin(t) = σ0(γstat(t), φstat(t), t) | (5.3.2) |
имеет прозрачный физический смысл. Это среднеквадратичная широтная невязка по рассматриваемой совокупности звезд в момент времени t, получившаяся после компенсации найденной систематической ошибки γstat(t), φstat(t). Как мы увидим далее, величина σmin(t) от времени практически не зависит ввиду крайне малой скорости собственного движения подавляющего большинства звезд. Поэтому мы будем использовать также обозначение σmin. Заметим, что до компенсации этой ошибки среднеквадратичная широтная невязка в момент t равнялась величине
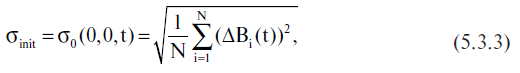
которая, вообще говоря, зависит от t. Таким образом, разность Δ σ(t) = σinit(t) — σmin(t) оценивает эффект от компенсации систематической ошибки γstat(t), φstat(t).
Далее при определении величин γstat(t) и φstat(t) из соотношения (5.3.1) момент времени t будем предполагать фиксированным. Поэтому аргумент t в выкладках мы опускаем, то есть, будем писать Li вместо Li(t),\; sb вместо sb(t) и т.д.
Для нахождения минимума в соотношении (5.3.1), возьмем частные производные функции σ02(γ, φ, t) по γ и φ и приравняем их нулю. С учетом формулы sin(Li + φ) = sin Li cos φ + cos Li sin φ, получим уравнения
| sb cos φ + cb sin φ = γ [s2 cos2 φ + 2 d cos φ sin φ + c2 sin2 φ], | (5.3.4) |
| -cb cos φ + sb sin φ = γ [-d cos2 φ + (s2 — c2) cos φ sin φ + d sin2 φ]. | (5.3.5) |
Разделив уравнение (5.3.4) на (5.3.5), получим
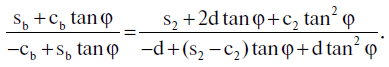
Приведя обе части этого равенства к общему знаменателю, приходим к следующему уравнению относительно tan φ:
(1+tan2 φ)(cbs2 — sbd) + (1 + tan2 φ) tan φ (cbd — sbc2) = 0.
Отсюда легко найти тангенс оптимального значения φstat:

Равенство (5.3.6) позволяет однозначно определить φstat, после чего оптимальная величина γstat может быть найдена, например, из (5.3.4):
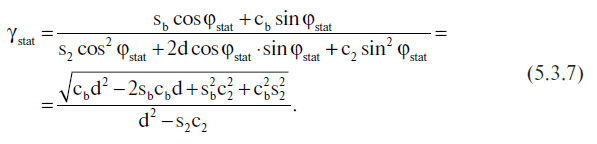
Формулы (5.3.6) и (5.3.7) дают искомое решение задачи нахождения оценок γ;stat и φ;stat методом наименьших квадратов.
Полезно провести анализ чувствительности в этой задаче. Рассмотрим частные производные второго порядка функции σ2(γ, φ, t); по γ и φ:
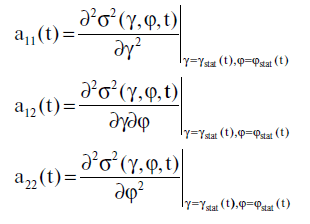
Учитывая равенства (5.3.4)—(5.3.7), нетрудно получить для этих частных производных следующие выражения:
| a11 = 2(s2 cos2 φstat + 2d cos φstat sin φstat + c2 sin2 φstat) = (2/γstat)(sb cos φstat + cb sin φstat), | |
| a12 = 2(cb cos φstat — sb sin φstat), | (5.3.8) |
| a22 = 2γ2stat(s2 sin2φstat — 2d sin φstat cos φstat + c2 cos2 φstat). |
Для оценки погрешностей в определении величины среднеквадратичной ошибки σ(γ, φ, t) при отклонении значений γ и φ от найденных оптимальных величин γstat и φstat воспользуемся следующим разложением функции σ2(γ, φ, t) в окрестности точки (γ(t), φ(t)):
| σ2(γ, φ, t) ≈ σ2min + a11(t) (γ — γstat(t))2 + 2a12(t)(γ —γstat(t))(φ — φstat(t)) + a22(t)(φ — φstat(t))2. | (5.3.9) |
В последней формуле мы пренебрегли членами третьего и более высоких порядков малости по отношению к разностям γ — γstat(t) и φ — φstat(t).
Формула (5.3.9) позволяет элементарными средствами оценить чувствительность среднеквадратичной ошибки σ(γ, φ, t) к вариациям параметров γ и φ. Для этого достаточно определить величины a11, a12 и a22, входящие в правую часть (5.3.9). После вычисления оценок γstat(t) и φstat(t) их легко найти по формуле (5.3.8).
Формула (5.3.9) показывает, что «линии уровня» среднеквадратичных ошибок являются эллипсами на плоскости (γ, φ). См. рис.5.3. Центром эллипса является точка (γstat, φstat), в которой значение среднеквадратичной ошибки равно σmin.

Направления осей эллипсов и соотношение между ними определяются стандартными формулами аналитической геометрии через величины a11, a12, a22, а именно, угол наклона α одной из осей эллипса определяется соотношением:
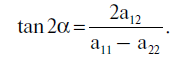
λ2 — λ (a11 + a22) + (a11 a22 — a212) = 0.
p/s
В квадратных скобках [] цифры обозначают порядковый номер источника; название источника читайте кликнув по ссылке ЛИТЕРАТУРА.
Уверен что данная книга ЗВЁЗДЫ СВИДЕТЕЛЬСТВУЮТ достойна быть настольной книгой всякого астронома, включая любителей.
Я не учёный, только учусь. /администратор сайта/
ЛИТЕРАТУРА: Данный список и его нумерация едины для цикла книг по Новой Хронологии.




![Рис.11.41. "Античная" мозаика в синагоге якобы VI века н.э. Эта мозаика (Beth-Alpha, Hefzibah), считается выполненной в византийской традиции с еврейскими надписями [1177], с.266. Изображен Зодиак и четыре времени года по углам. В центре мозаики, как пишут историки, помещен Бог-Солнце в короне (в греко-римской традиции), справа от него - полумесяц, а вокруг - 23 звезды. Бог управляет четверкой лошадей. Мы видим, что Зодиаки изображались не только в "древне"-египетских храмах, но и, например, в синагогах. Взято из [1177]. илл.15.4, с.267.](https://proshloved.ru/wp-content/uploads/2023/07/ris.-11.41-345x230.jpg)


![Рис.11.37. Старинное изображение системы мира по Тихо Браге. Это в точности - ГЕЛИОЦЕНТРИЧЕСКАЯ СИСТЕМА, где начало координат помещено в Землю. Взято из [946], с.151.](https://proshloved.ru/wp-content/uploads/2023/07/ris.-11.37-345x230.jpg)

